Term Rewriting

Language definitions are often based on significant tacit knowledge. For example, the C array vs struct definitions refer to contiguously allocated vs sequentially allocated memory. Many C programmers would have trouble explaining that.

Our aim is to define an entire programming language without any prerequisites other than precision. No turtles required.

Sets of Turtles

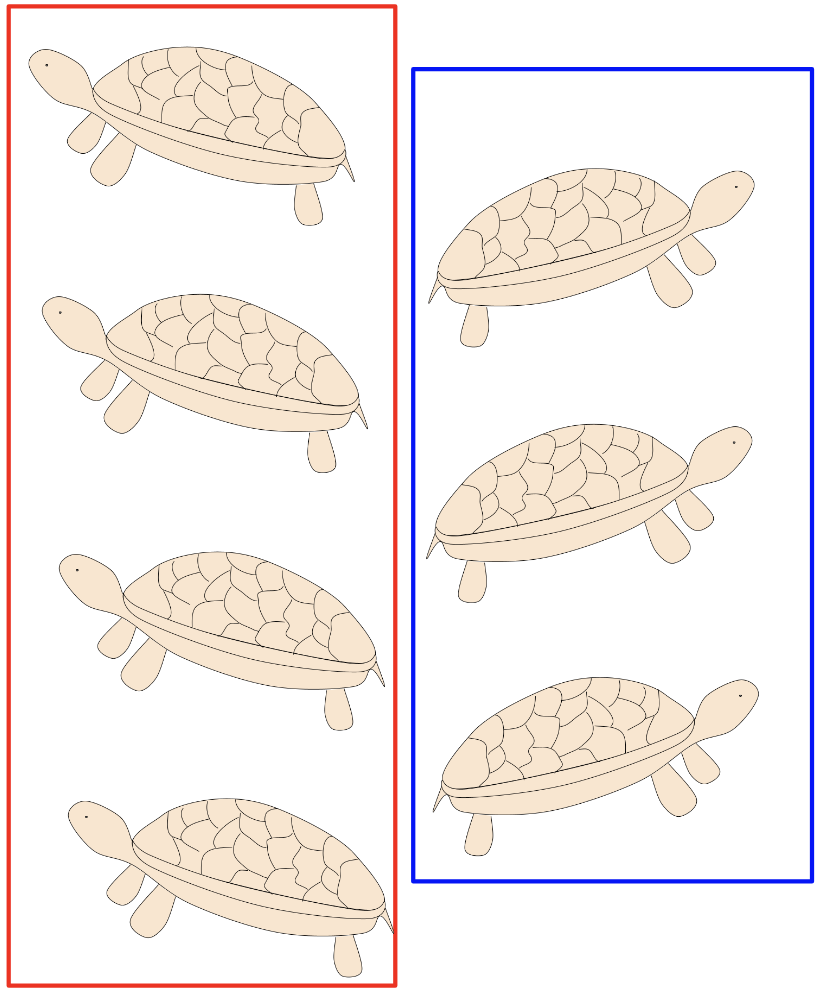
Consider these seven turtles. It is easy to imagine

• the set of right-facing turtles (blue box)
• the set of left-facing turtles (red box)
• the union (the entire set of seven)
• the intersection (empty)

Do we need turtles to talk about sets? No. We can define sets without turtles. Naive sets are sufficient (that is, equality if they have the same elements, union, intersection)

We have already seen one set without turtles: the empty set, written as {}. To be clear: there is almost no presumption here, just notation. All we presume is the empty set, not containing turtles or anything else. Let’s give this set a name: 0, so 0 = {}

Unbounded numbers of sets

Now consider a set with exactly one element: the only thing we know so far, which is the empty set {}. This set is {{}}, and for clarity, we’ll name it 1. Clearly, 1 ≠ 0 because 1 has an element, and 0 doesn’t. So now we now know two sets!

The next set we might consider is {0,1}, the set containing the two things we know so far, that called 0 and 1. We could also have written {{},{{}}} (this is why we give our sets names; braces are pretty soon unintelligible for humans).

This set {0,1} is again a new set because it has one more element than 1. And it reveals a pattern: given sets 0, … ,N, the set {0, … , N} is a new set which we call N+1. Again: the use of names and numbers is a convenience – we do not presume the existence of numbers. As a matter of fact, using sets is a valid way to define numbers.

So, without significant presumptions, there is an unbounded number of unequal sets. We’re avoiding the notion of infinity (which we don’t need). In addition, we forego the precise definition of sets; for our purposes, the naive definition is sufficient. But in all fairness, we did make a presumption, which is: reasoning about finite sets.

Sets and Values

Starting from nothing, we have described mental artifacts called sets. We have given a sequence of these the names 0, 1, 2, etcetera, so there is an unbounded number of them. Note that there are many more sets than the ones we have given names, such as, for instance: {1, 3, 10}. To distinguish the named sets from the unnamed sets, we will call the named sets: values. The unnamed sets will still play a role in our discourse.

It is easier for us to talk about values such as 3 than to talk about sets such as {{},{{}},{{},{{}}}}. But we haven’t presumed numbers; we just reason about named sets.

Representation

As it happens, computers are rather good at storing and processing numbers represented as strings of bits in a format that is called binary. The relation between stored numbers and the real numbers (which are also a mental construct) is by convention. The view that 101 is related to the number 5 is just as sensible (albeit more common) as the view that it might be related to the set 5 (which is {{{}},{{},{{}}},{{},{{}},{{},{{}}}}, {{{}},{{},{{}}},{{},{{}},{{},{{}}}}}}).

Conceptually we are still within the theory of sets, but values (which are sets) can be represented as bits and bytes and binary numbers and can be processed by computers.

Sets as Larger Constructs

Now we will discuss several concepts based on the sets we have seen so far.

Pair, Tuple

Given two sets a and b the pair <a,b> is the set {a,{a,b}}. A pair is not a new concept but a notation. Note that from a pair, the constituent two elements can be unequivocally determined. A pair is a set of two elements, one of which is again a set with two elements. The larger and the smaller set have an element in common, which is the first constituent of the pair. The second element of the smaller set is also the second constituent of the pair.

If you are a programmer and unused to thinking about sets: a pair is somewhat like a C struct or JavaScript list.

Given N values v1, …, vN a tuple <v1, …, vN> is defined similarly to a pair. A tuple is a set from which the N constituents can be retrieved, so it is again similar to a struct or list.

Relation, Function

A relation is a set of pairs. Example: {<1,2>,<1,3>,<2,3>} is a relation. Note that we are mixing notations to remain intelligible: the braces {...}, brackets <...>, and numbers 1 notations. Just using braces, this example becomes:
{{{{}},{{{}},{{},{{}}}}},{{{}},{{{}},{{},{{}},{{},{{}}}}}},
{{{},{{}}},{{{},{{}}},{{},{{}},{{},{{}}}}}}}

Probably you are used to relations such as ≤ (less-than-or-equal). This is the same thing: {<1,1>,<1,2>,<1,3>,<2,2>,<3,3>,<3,3>} is the relation ≤ on the numbers 1, 2 and 3. As an aside, also note that this relation can also be defined as the ‘is contained in’ relation ∈ because n<m (less than) if and only if n∈m (is contained in) considering n and m as names of sets.

A function is a relation in which each first value in the pairs is unique: the relation {<1,1>, <1,2>, <2,2>, …} is not a function.

The notation f(x) and R(x,y)

The notation f(x): given a set of pairs f and a value x, f(x) denotes the value for which <x,f(x)> occurs in f. Similarly, R(x,y) means that <x,y>∈R.

A function f is a set of pairs, and f(x) selects a value contained in f. A programmer tends to think of f(x) as f being applied to or acting on x. There is nothing wrong with this view, but remember that underlying it is a statement about sets.

Symbols, Variables

Now consider two disjoint sets of values S={s1, …, sN} and V={v1, …, vM}. We’ll call each si a symbol and each vi a variable. There are no restrictions on the sets of values and symbols. For example, one might choose the set of symbols to be all odd-named values and the set of variables all even-named values.

We give symbols and variables names (identifiers). By convention, an identifier starting with:

• an upper case letter is a variable: e.g. X, Bar
• a lowercase letter is a symbol: e.g. f, aX

Note that naming symbols and values is similar to middle-school practice for algebra and geometry. Consider the statement: x=½π. Here, x is the name of a variable, and π is the symbol used for the ratio between the diameter and the circumference of a circle.

Note: symbols and variables are values (sets) and can be represented as binary numbers.

Terms

A term is either a variable or a tuple <f,t1, …,tk> (for k ≥ 1) where

• f is a symbol
• Each ti is a term

Confusingly, in our text, we also give names to terms, such as t. It should be clear from the context whether an identifier refers to a symbol or to a term.

The pair-notation isn’t used for terms; we use the special notation f(s1, …, sk).

If f has no arguments, no parentheses are used: we write f instead of f() (again confusingly; but it should be clear from context whether we mean symbol f or term f).

Given a term t=f(s1, …,sk), the symbol f is called the outermost function symbol of t

Sub-term, Open / Closed Terms, Constant

Each si is a sub-term of f(s1, …,sk), and all sub-terms of each si are also sub-terms of f(s1, …,sk).

An open term is a term that contains variables; a closed term doesn’t.

A closed term without sub-terms (e.g. f) is called a constant (somewhat confusingly, since any closed term is in a way a constant because it doesn’t contain a variable, but there it is)

Trees

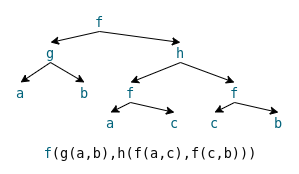
When terms are drawn, they appear tree-like as a structure of nodes and edges. In this sense, we often refer to the outermost level (the highest level or top) as the rootand to the innermost (lowest) level as leaves.

Substitution, Instantiation, Matching

A substitution is a function mapping variables to terms (i.e., set of pairs <vi, si> where each vi is a unique variable, and each si is a term).

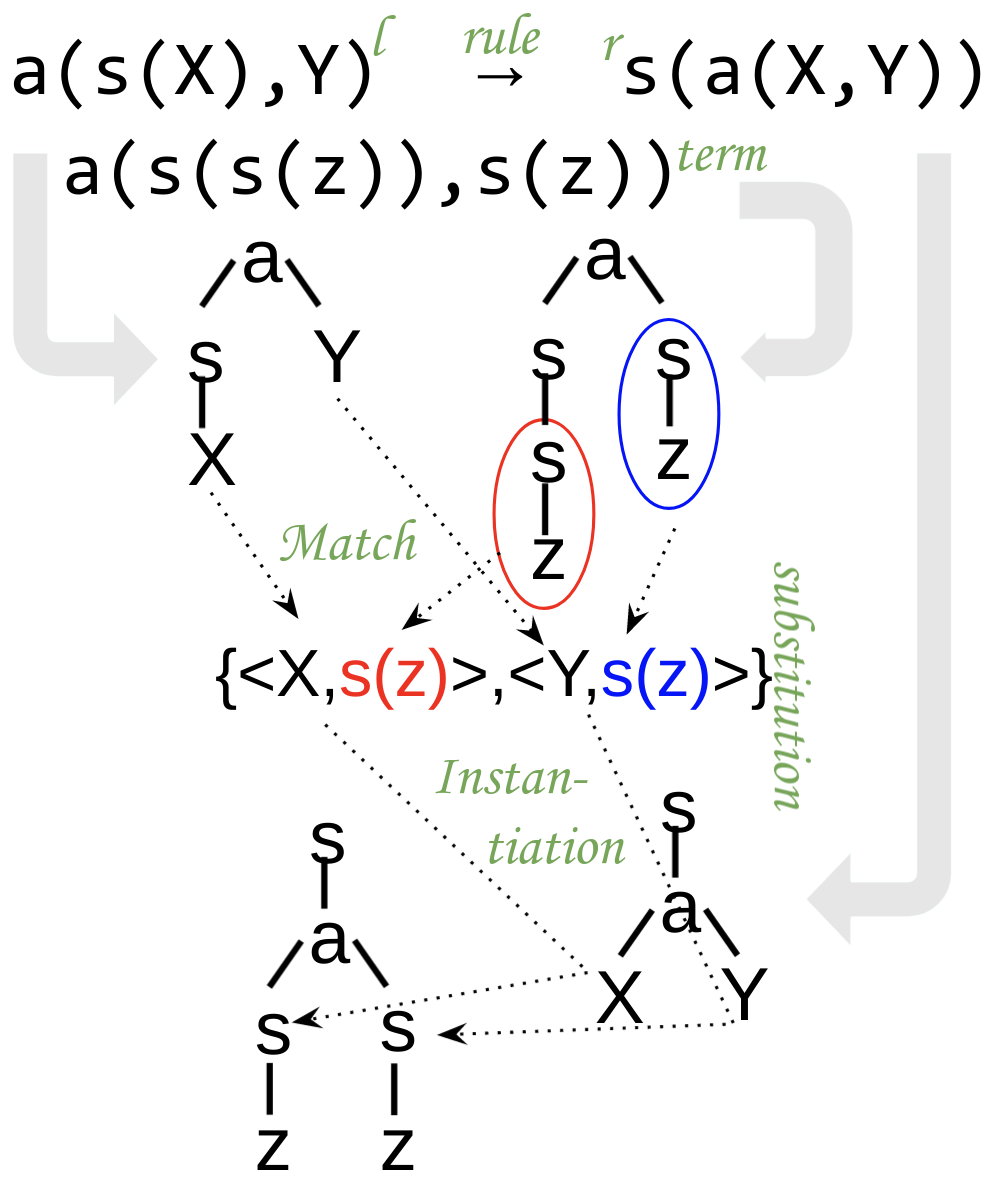
An open term t can be instantiated with a substitution S by replacing variables in t with their S-value.

For example: instantiating s(a(X,Y)) with {<X,s(z)>,<Y,s(z)>} produces s(a(s(z),s(z))).

Given a closed term such as t=a(s(s(z)),s(z)) and an open term such as p=a(s(X),Y), matching tries to find a substitution S such that S(p)=t. Matching can either fail or succeed in producing a substitution.

Rules, Term Rewriting Systems

A rewrite rule is a pair of terms written as lhs → rhs where

• lhs has at least one symbol (i.e., isn’t a sole variable)
• every variable in lhs occurs at most once
• every variable in rhs also occurs in lhs

Given a rule, lhs → rhs, lhs and rhs are called the left-hand side and the right-hand side, respectively.

A term t can be rewritten to a term u by rule lhs → rhs if a substitution S exists such that t=S(lhs) and u=S(rhs). Rewriting is a relation (called the rewrite relation), and by convention, we write it as t → u (confusingly, the notation for rules and for the rewrite relation are the same). That is: given a rewrite rule, lhs → rhs, ‘→’ is the rewrite relation between terms. In a more operational context, the rewrite-step relation is also called reduction.

This relation can be extended in an obvious way by rewriting sub-terms:
if t → u and if t is a sub-term of v, then v → w when w is obtained from v by replacing that sub-term t in v by u. A more precise definition follows in the last section of this page.

Secondly, the relation can be extended by regarding multiple rules at once: t → u if a rule l → r exists such that t → u for that rule.

A set of rewrite rules is called a Term Rewriting System (TRS).

To summarize, a term rewriting system defines a one-step rewrite relation (written as →) on terms, such that t → u means that

• a rule l → r exists in the TRS
• a substitution S exists
• t has a sub-term p
• S(p)=l
• q=S(r)
• u is obtained from t by replacing a sub-term p in t by q

The one-step rewrite relation can be transitively extended:
s ↠ t if, and only if s → t or s → u and u ↠ t. In other words: s ↠ t when a chained sequence of rewrite steps s → u, u → v, v → w … x → y, y → t, exist.

If s ↠ t and no rule is applicable to any sub-term of t (or t itself), t is called a normal form of s (or the normal form if there is only one).

Operationalization

It might seem that this document is turning into an abstract theoretical discussion. So let’s take a step back and see where we are and where we are headed.

Using only a naive sense of sets essentially founded only on the empty set, we have

• identified and named an unbounded number of sets, which we called values, and identified an even bigger collection of unnamed sets
• picked two disjoint collections, which we called symbols and variables
• sketched schemas to group sets in
  • pairs and tuples
  • relations and functions
  • terms, rules, and rewrite systems
• described the rewrite relation(s) on terms

This is all good and proper, but how can we implement it for practical use.

Before we do, we must make an operational choice.

To paraphrase ‘rewrite step’: given a TRS and a term, s → t

• if there is a rule l → r
• and if there is a sub-term p of s such that p matches l, then we can replace p with the corresponding instance of r to get t.

But what if more than one rule and sub-term exist for which this is the case? That is to say, what if given some term s, many terms t exist such that s → t or s ↠ t.

Strategies

1
2
3

f(a) → f(b)
f(b) → f(a)
a → c

A rewrite strategy determines which rule and which sub-term to pick.

Sub-Term Selection

The innermost and outermost strategies limit the location where reductions are considered. An innermost strategy reduces a sub-term only if all deeper sub-terms of that sub-term can not be reduced. An outermost strategy reduces only sub-terms of a term if they aren’t contained in a (sub-) term which is reducible at the root level.

Consider this TRS:

1
2
3

f(a) → f(b)
f(b) → f(a)
a → c

This TRS is terminating under an innermost strategy but not under an outermost strategy.

Now consider a function if for which two rules are given:

1
2

if(true,X,Y) → X
if(false,X,Y) → Y

Consider a term if(B,T,E) where B, T and E are given terms for a boolean expression, the ’then’ part and the ’else’ part. Clearly, any reduction in the then or else parts may prove to be irrelevant until the Boolean expression is reduced to either true or false.

If B proves to be true, any reductions in the else part were pointless (when one considers an implementation, superfluous reductions represent wasted time) and potentially harmful if the else part leads to infinite reduction sequences (which may not be a bug if B is true.

A safer and more optimal strategy (for instance, the left-most outermost reduction strategy) evaluates the Boolean, and only then reduces if.

Speaking generally, outermost strategies are ‘better behaved’ with respect to termination, but innermost strategies can be implemented more efficiently. While it is true that innermost strategies can lead to non-termination, it is generally straightforward to write a term rewriting system such that non-termination is avoided in the same way that infinite loops should and can be avoided in general programming languages.

Rule Selection

A second aspect the strategy must address is: if more than one rule is applicable at the same location, which is chosen? If the term rewriting system is confluent, it doesn’t matter in a sense. But it may be unknown if the term rewriting system is, in fact confluent if non-termination lurks, or, in an implementation, if one choice might be more efficient than another.

Common strategies which address this are specificity order and textual order.

• textual order always applies the first rule (in the textual representation of the TRS) that is applicable (to the sub-term under consideration);
• specificity order always applies a rule which is at least as specific as all other applicable rules. Specificity can be defined as the total number of function symbols on the left-hand side. Specificity order makes intuitive sense because otherwise, that more specific rule would never be considered!

As an example, consider a function iszero, which tests if a number in the a-s-z-system (see also at the end of this section) is zero.

1
2

iszero(N) → false
iszero(z) → true

Using textual order, this term rewriting system always returns false, but using specificity order, the implementation behaves appropriately.

To be honest, this TRS is unnecessarily confusing, especially for a programmer who is used to reading code from top to bottom. By convention, the order of rules is always given such that textual order and specificity order coincide as much as possible.

1
2

iszero(z) → true
iszero(N) → false

Notation

So far, we have used this notation l → r for rules.

1
2

iszero(z) → true
iszero(N) → false

But the symbol → doesn’t occur on any keyboard, and the lack of a separator between rules might lead to difficult-to-read code.

We will use the symbol = instead of → in rules and terminate all rules with ;.

In this document, rule numbers are often included for reference. They are not part of the spec but only of the presentation.

The above TRS would then appear as:

1
2

iszero(z) = true;
iszero(N) = false;

The use of = (equality) deserves a comment: rewrite rules and rewriting are directional, always being applied from left to right. On the other hand, they do express equality. The predicate iszero applied to z is rewritten to true precisely because iszero(z) is (equal to) true. Rewriting is syntactical simplification within semantical equality.

Example

Consider the following TRS (’the a-s-z-system’; successor-zero with addition):

1
2

a(s(X),Y) = s(a(X,Y));
a(z,X) = X;

and consider the following sequence of rewrite steps:

a(s(s(z)),s(s(z))) 
→ s(a(s(z),s(s(z)))
→ s(s(a(z,s(s(z)))))
→ s(s(s(s(z))))

Now, interpret

• z as zero
• s as successor (plus one)
• a as add

We have just defined addition for unsigned integers!