Booleans

There are two values: true and false. Many operations, such as comparisons, on other data (e.g. numbers, dates) result in a boolean. For instance: x>5 is true if x exceeds 5 and is false otherwise.

Truth values can be combined or computed using Boolean operators.

AND yields true only if both its arguments are true, and yields false otherwise (i.e. if one argument or both are false).

For example, for example, you can only join this park ride if your length is between 1.40 and 2.10, and your weight does not exceed 150Kg. canJoin = (len > 1.40 AND len < 2.10) AND weight < 150

Other operators include OR, NAND, NOR and NOT.

Boolean Arithmetic

It is sometimes convenient to represent Boolean values as numbers: 0 (false) and 1 (true). A single bit can be interpreted as an integer or as a Boolean.

When 0 and 1 are used to represent truth values, the AND operator is often written as * . Note that multiplication, when limited to 0 and 1, does indeed compute AND: p * q only equals 1 if both p and q are 1.

Similarly, OR is written as + and NOT is written as unary -. Note that Integer and Boolean + and (unary) - do not coincide with the integer operations: Boolean 1+1 is 1 and -1 is 0.

In many programming languages, AND and OR are often written as & and |.

In programming, identifiers true and false are generally used to avoid confusion with integers, although in many languages integers can be used as ’truth values’.

Truth Tables

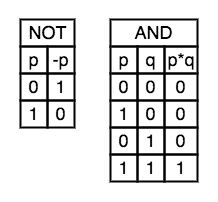
Truth Tables are a technique to compute the value of Boolean expressions. In a truth table all possible values of all variables are listed together with the value of the expression (or its sub-expressions if the expression is complex).

The truth table of NOT and AND are:

Complex Truth Tables

Using truth tables, the value of complex Boolean expressions can be computed even if their value isn’t obvious immediately. For instance: what is the value of

(p or q ) and not (not p and not q) 

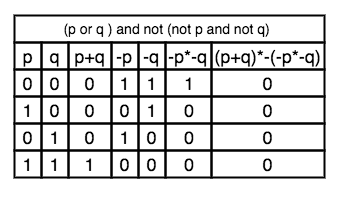
Without the truth table it is not immediately clear that this expression is always false.

An important operator is XOR (exclusive or): p xor q = (p or q) and not (p and q).

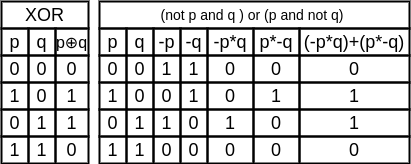
This operator is important because unlike AND and OR it does not lose information and is therefore useful in encryption: (p xor q) xor p = q. To the right is a common symbol for an XOR gate.

Consider the truth tables of (not p and q) or (p and not q) and p xor q. From the tables, we see that they are identical!

Binary Numbers

Most people today use the Arabic Numeral System based on ten digits, which is a positional numbering system where the contribution of a digit to a number is determined by the digit and by its position in the number. So even though the ‘1’ in ‘12’ is a smaller digit than the 2, its contribution is larger because of its position. To be precise: there are 10 digits, so the largest single-digit number is 9. The next number can not be represented using a single digit, so two digits are used: the smallest non-zero digit followed by zero; 10. The ‘weight’ of the position of the 1 is equal to the number of digits (i.e. ten) so the total value is ten.

Using ten digits at hardware level is impractical, but using two digits does make sense: the digits 0 and 1. Binary also has a number 10, but the weight of the 1 equals now equals two (the number of digits).

Note the difference between a number and its representation(s):
This is a number of dots …. …. ….

• In decimal, the number of dots is written as: 12
• In binary it is written as: 1100
• In hexadecimal (which we will revisit) it’s written as: c

Binary to Decimal Conversion

Conversion from binary to decimal is very simple.

• write down the weights of as many digits as you need
• for every digit 1, add the corresponding weight

For instance, to convert 1001 to decimal, write the weights: 8,4,2,1 (each position the weight is multiplied by two). There are ones at the first and last position so the value is 9.

Note that the weight of the n-th position from the right is 2^n, the n-th power of 2.

Decimal to Binary Conversion

To convert a decimal number to a binary number do the following:

1. if the number is even, write down a 0
2. if the number is odd, write down a 1 and subtract 1 from the number
3. divide the number by two
4. goto step 1 unless you have reached 0

The digits you have written down are the binary digits from right to left.

For instance: convert 91

(91) 1 (45) 1 (22) 0 (11) 1 (5) 1 (2) 0 (1) 1 (0)

Binary: 1011011 (check: 1+2+8+16+64=91)

Exercises:

1. Convert the binary number 101 to decimal
2. Convert the decimal number 101 to binary

⊙

Binary Arithmetic

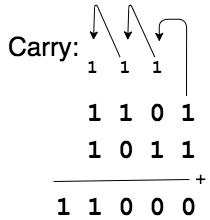
Exactly the same rules and methods exist for binary arithmetic as for decimal arithmetic: 1 + 1 can’t be 2, so it is 10; that is 0 with a carry 1.

For instance, this is the addition of 1101 and 1011 (check: 13 + 11 = 24).

The tables of multiplication are trivial, so multiplication is a matter of rigorous discipline:

   110
   101
 ----- *
   110
 11000
  ---- +
 11110 (check => 2+4+8+16 = 30)